In the previous post, we studied multi-headed attention mechanisms. In this post, we will look into the details of Graph Attention Networks. Due to their flexibility and versatility that easily allow us to capture complex relationships between data points, Graphs make very useful data structures. In fact, a number of important real-life datasets are composed of graphical structures: Social Networks, Brain Connectomes, Image Scene Graphs etc. Being able to find the underlying patterns in this kind of data is therefore an important direction for machine learning research.
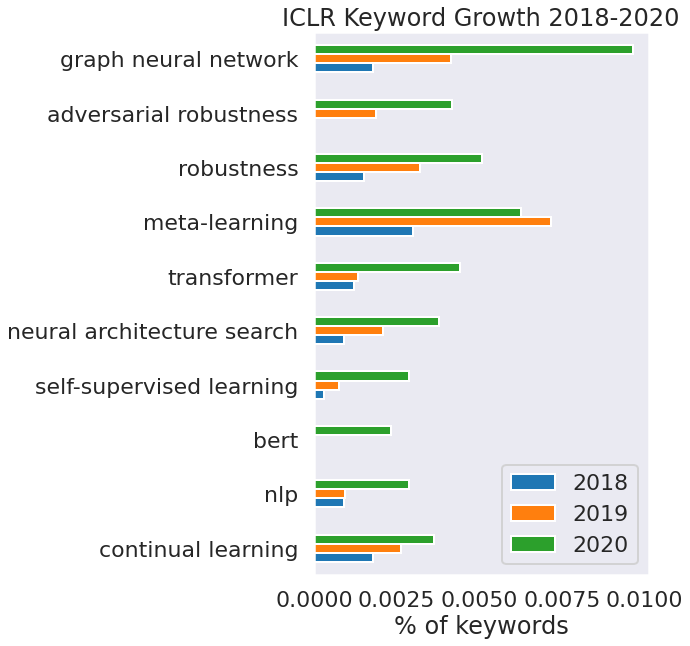
Picture Source: @srush_nlp
The above plot demonstrates the booming affection of machine learning research community towards Graph Neural Networks. In this blog, we will discuss Graph Attention Networks(GATs), a breakthrough in learning representations from graphical structures.
The Problem Description
Given a graph \(G\), consisting of a set \(V\) of \(n\) nodes (vertices), represented by the feature vectors \(\{v_1, v_2,...,v_n\}\), and an adjacency matrix \(\mathbf{A}\), such that \(\mathbf{A}_{ij} = 1\), if the nodes \(i\) and \(j\) are connected, 0 otherwise. Typically, \(\mathbf{A}_{ii} = 1 \forall i \in \{1,2,...,n\}\). The task is to obtain a set of new node features \(V' = \{v_1', v_2',...,v_n'\}\), based on the input features and the graph structure. Mathematically,
\[V' = \mathcal{F}\large(V, \mathbf{A} ; \theta \large)\]Where \(\mathcal{F}\) is a transformation parameterized by \(\theta\).
A graph can be arbitrarily large, therefore, to keep the total number of parameters \(\|\theta\|\), finite, we require \(\|\theta\|\) to be independent of the input graph size. It is plausible to assume that the neighbours of a node play a crucial role in influencing it’s properties, therefore, for a node \(i\), we require that it’s resultant features are dependent on the input features of the nodes in it’s neighbourhood (Localization). To ensure flexibility, the transformation should be able to assign arbitrary importances to different neighbours. Also, the transformation should not be dependent on a particular graph structure to extend it’s applicability to unseen graphs.
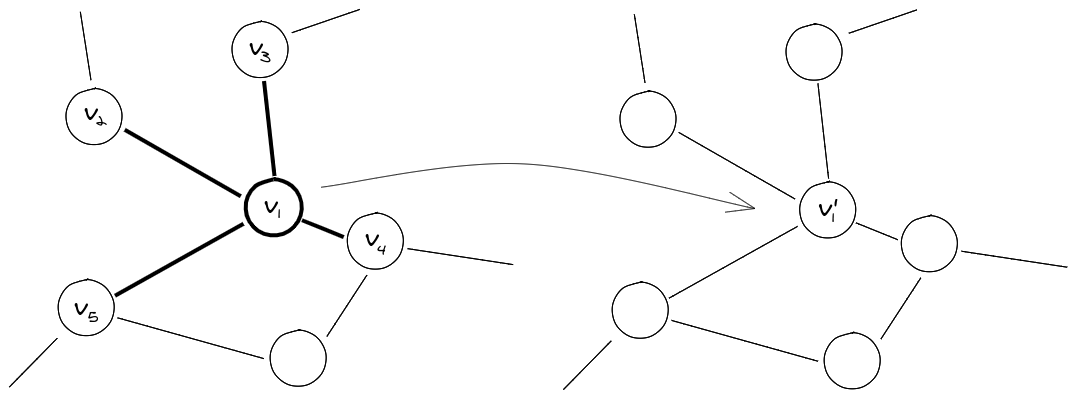
Fig 1: A rough sketch of the desirable form of the solution, shown for a single node
Graph Convolution Networks
To obtain a higher level reprsentation of each node while maintaining a finite number of parameters, every graph convolutional layer starts off with a shared node-wise feature transformation specified by the weight matrix \(W\). For node \(i\)
\[u_i = Wv_i\]To satisfy the localization property, the graph convolution operator is usually defined as an aggregation of features across neighbourhoods; defining \(\mathcal{N}_i\) as the neighbourhood of node \(i\), the features of this node can be updated as
\[v'_i = \sigma\left(\displaystyle\sum_{j\in\mathcal{N}_i} \alpha_{ij}u_j\right)\]Where \(\sigma\) is an activation function and \(\alpha_{ij}\) specifies the relevance of node \(j\) to the node \(i\).
Prior to the GATs, most of the work done on graph covolution networks specified \(\alpha_{ij}\) explicitly, either based on the structural properties of the graph or as a learnable weight, which requires compromising at least one desired property. GATs on the other hand employ a self-attention mechanism over the neighbourhood nodes to find each of their relevance scores.
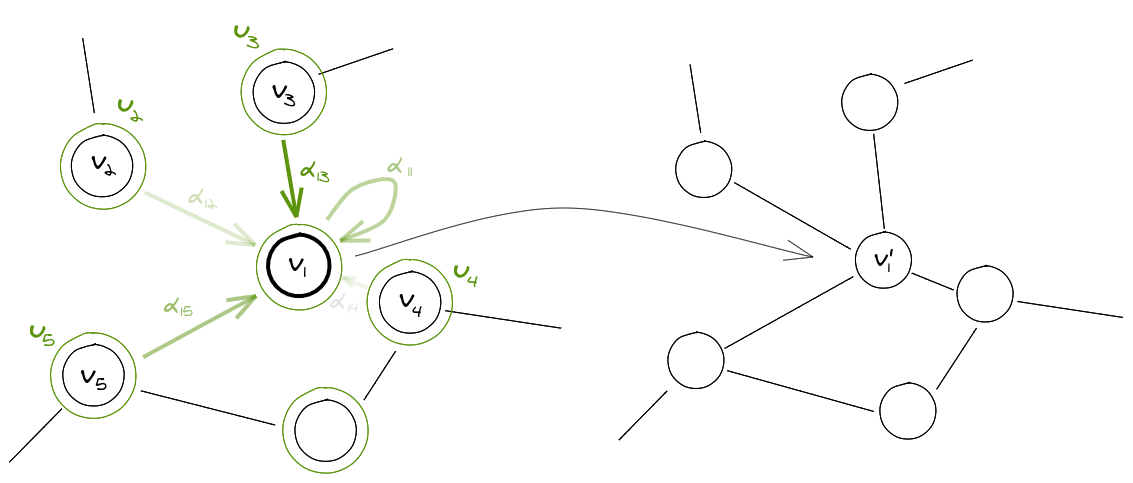
Fig 2: A depiction of the graph convolution operator.
Improving the Graph Convolution: Graph Attention Networks
Taking inspiration from Vaswani et al., graph attention networks leverage self-attention over the neighbourhood nodes to find the updated feature representation of a node. For an attention mechanism \(a: R^\mathbf{N} \times R^\mathbf{N}\), the relevance score between a pair of nodes \(i,j\) can be calculated as
\[e_{ij} = a(v_i, v_j)\]These relevance score are then normalized across the neighbourhood
\[\alpha_{ij} = \frac{\text{exp}(e_{ij})}{\sum_{k \in \mathcal{N_i}} \text{exp}(e_{ik})}\]While the approach is agnostic to the choice of attention mechanism, the authors employ a single layer neural network on the concatenation of input vectors to calculate relevance scores.
Multi-Headed Graph Attention and Regularisation
The authors mention that they find multi-headed attention beneficial to stabilize the learning process of the self-attention mechanism. Basically, the above operations are independently replicated \(K\) times (each replica with different parameters) and the outputs are aggregated either by concatenation or by averaging.
\[v'_i = {\Bigg|\Bigg|}_{(k=1)}^K \sigma\left(\displaystyle\sum_{j \in \mathcal{N}_i} \alpha_{ij}^k W^kv_j\right)\]Where \(\alpha_{ij}^k\) is the relevance score between the node \(i\) and \(j\) determined by the \(k\)-th replica and \(W^k\) is the weight matrix specifying the transformation for the \(k\)-th replica.
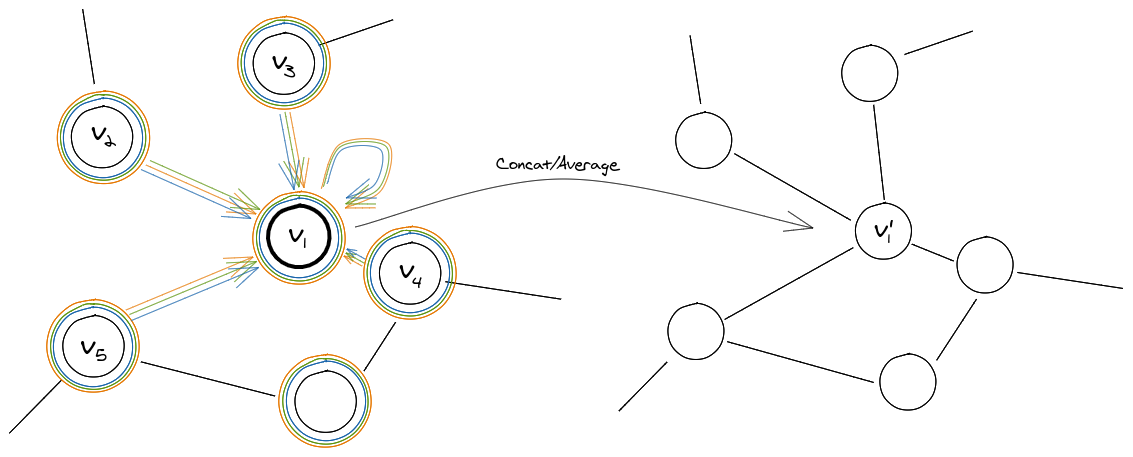
Fig 3: The process depicted in Fig 2 is replicated K times for the multi-headed variation. Here K=3.
Although, the idea for using multiple heads is inspired from Vaswani et al., the execution is slightly different. Vaswani et al. divided every input feature vector into \(K\) chunks where \(K\) is the number of heads, and self-attention was individually applied over each chunk, whereas in GATs, every node feature is copied \(K\) times, and then the attention mechanism is individually applied over each copy.
Furthermore, it is mentioned in the paper that applying dropout to the attention scores (dropping some of the nodes during weighted aggregation after the attention scores are calculated) to be a highly beneficial regularizer, especially for smaller training datasets.
The presented Graph Attention Networks satisfy all the desirable properties for a graph convolution. Parallelization using the adjacency matrix makes a GAT layer computationally efficient. Parameter sharing across nodes allows the total number of parameters to be independent of the graph size. Node features are updated on basis of the neighbourhood, which satisfies the localization property. Also, GATs can be used over any type of graphs, thus the structure of graph does not affect the way a GAT layer is applied. Attention mechanisms also add the factor of interpretability which is really helpful.
Acknowledgement and Additional Resources
I would like to thank Petar Veličković for his awesome blog on Graph Attention Networks. Do check that out.
Graph Representation Learning is a wide domain with every conference witnessing a large number of submissions in this field each year. The aim of this blog was to demonstrate how attention mechanisms were first employed on graphical structures. If you are interested in learning more about graphical representation learning kindly checkout this Twitter thread from Petar.
References
- Veličković, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., & Bengio, Y. (2018). Graph Attention Network, International Conference on Learning Representations.
- Vaswani, A., Shazeer, N., Parmar, J., Jones, L., Gomez, L., & Polosukhin, I. (2017). Attention Is All You Need arXiv e-prints, arXiv:1706.03762.
- Petar Veličković’s Blog on Graph Attention Networks
Cited as:
@article{nikhil_attention,
title={Attention! An Other Perspective},
url={https://learningturtle.github.io/Blog/posts/attention_another_perspective_part5/},
journal={Learning Turtle},
author={Nikhil},
year={2020}
}
Postscript
If you find any mistakes/complicacies in our blogs or if you have any suggestions/feedback, do not hesitate to contact us at learningturtle.yt@gmail.com.